write a program to check whether entered number is prime or not.....

 Check whether entered number is prime or not.....

#include<iostream.h>
#include<conio.h>
        void main()
        {
         //clrscr();
         int number,count=0;
cout<<"ENTER NUMBER TO CHECK IT IS PRIME OR NOT ";
          cin>>number;
           for(int a=1;a<=number;a++)
               {
                if(number%a==0)
                   {
                  count++;
                   }
               }
       if(count==2)
         {
          cout<<" PRIME NUMBER \n";
         }
       else
         {
          cout<<" NOT A PRIME NUMBER \n";
         }
       getch();
       }

Trees In Graph Theory........

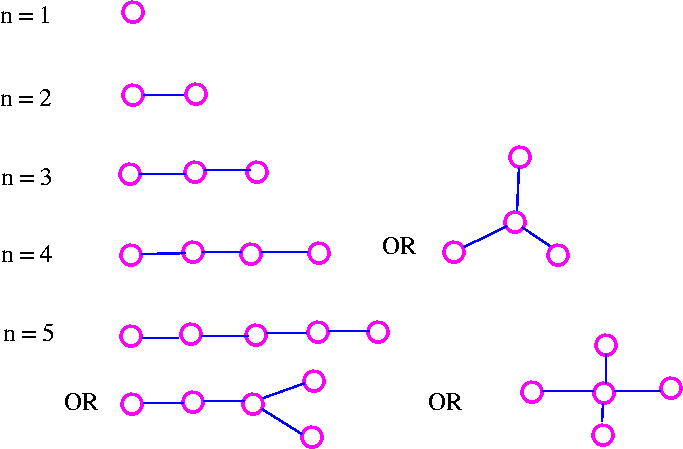
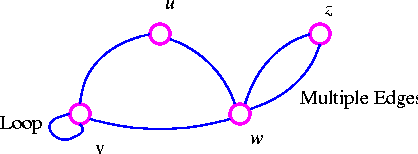
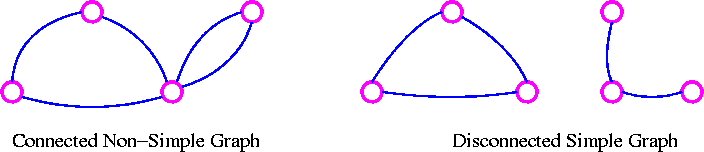
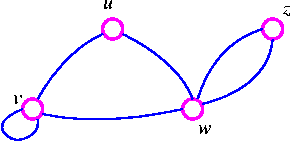
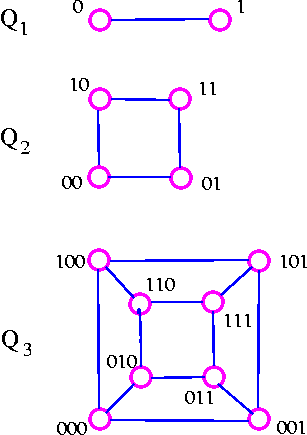
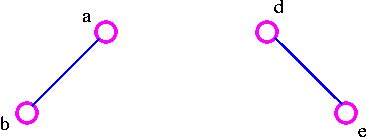Trees

An acyclic graph (also known as a forest) is a graph with no cycles. A tree is a connected acyclic graph. Thus each component of a forest is tree, and any tree is a connected forest.

Theorem    The following are equivalent in a graph G with n vertices.

1. G is a tree.
2. There is a unique path between every pair of vertices in G.
3. G is connected, and every edge in G is a bridge.
4. G is connected, and it has (n - 1) edges.
5. G is acyclic, and it has (n - 1) edges.
6. G is acyclic, and whenever any two arbitrary nonadjacent vertices in G are joined by and edge, the resulting enlarged graph G' has a unique cycle.
7. G is connected, and whenever any two arbitrary nonadjacent vertices in G are joined by an edge, the resulting enlarged graph has a unique cycle.

Generally speaking, algorithms associated with trees can be divided into three types.

• Algorithms for searching and labeling a given tree.
• Algorithms for constructing various types of tree.
• Algorithms for counting trees of a particular type.

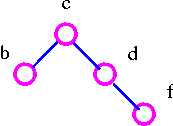
Tree    A tree is a connected graph which contain no cycles.
For example,

Theorem    Let T be a graph with n vertices. Then the following statements are equivalent.

1. T is connected and contains no cycles.
2. T is connected and has n-1 edges.
3. T has n-1 edges and contains no cycles.
4. T is connected and each edge is abridge.
5. Any two vertices of T are connected by exactly one path.
6. T contains no cycles, but the addition of any new edge creates exactly one cycles.

Spanning Trees
Let G be a connected graph. A spanning tree in G is a subgraph of G that includes all the vertices of G and is also a tree. The edges of the trees are called branches.
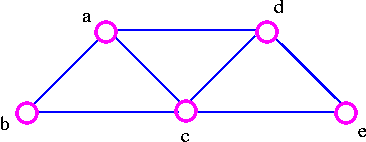
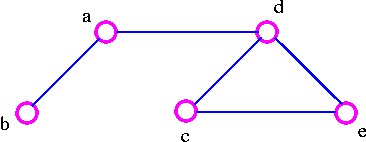
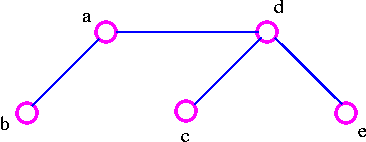
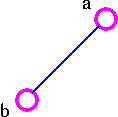
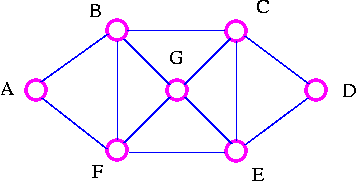
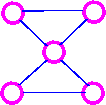
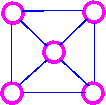
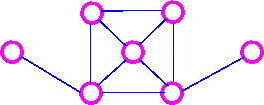
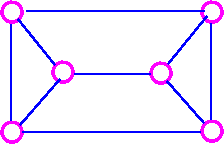
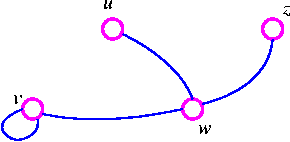
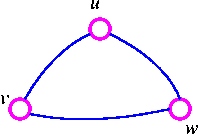
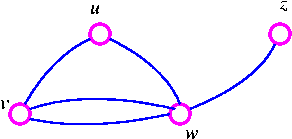
For example, consider the following graph G

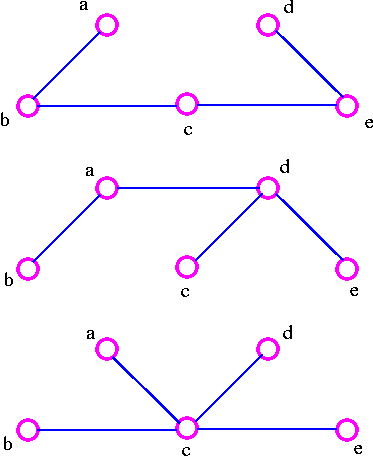
The three spanning trees G are:

We can find a spanning tree systematically by using either of two methods.

• Cutting-down Method
  • Start choosing any cycle in G.
  • Remove one of cycle's edges.
  • Repeat this procedure until there are no cycle left.

       
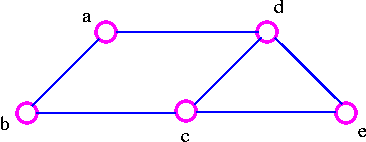
                For example, given the graph G

                1. We remove the edge ac which destroy the cycle adca in the above graph and we get

                2. We remove the edge cb, which destroy the cycle adcba in the above graph and we get

                3. We remove the edge ec, which destroy the cycle decd in the above graph and thus obtained the following spanning tree.

• Building-up Method
  • Select edges of G one at a time. in such a way that no cycles are created.
  • Repeat this procedure until all vertices are included.

                For example, for the following  graph G

                1. Choose the edge ab

                2. Next choose the edge de as follows:

                3. After that choose the edge ec as follows:

                4. Finally, we choose the edge cb and thus obtain the following spanning tree.

Theorem     A graph is connected if and only if it has a spanning tree.

Proof    Let G be a connected graph. Delete edges from G that are not bridges until we get a connected subgraph H in which each edge is a bridge. Then H is a spanning tree. On the other hand, if there is a spanning tree in G, there is a path between any pair of vertices in G; thus G is connected.



Centers and Bicenters
It is convenient to start building up the tree at the middle of a tree and move outwards. This was the approach used by Arthur Cayley when he counted the number of chemical molecules by building them step by step. But what do we mean by the "middle" of a tree?
There are two straight forward ways to compute centers and bicenters.

Algorithm1

• Remove all the vertices of degree1, together with their incident edges.
• Repeat the process until we obtain either a single vertex (the center) or two vertices joined by an edge (the bicenter).

A tree with a center is called a central tree, and a tree with a bicenter is called a bicentral tree. Note that every tree is either central or bicentral, but not both.
For example, given a following tree.

Remove all vertices of degree 1.

Remove all vertices of degree 1.

Therefore, a tree is central with center e.

Another example, given a following tree.

Remove all vertices of degree 1.

Remove all vertices of degree 1.

Therefore, a given tree is bicentral with bicenter cd.

Algorithm 2
For each vertex v of the degree 2 or more, count the number of vertices in each of the subtrees emanating from v, and let n_v be the maximum of these numbers. If the tree has nvertices it can be shown that either there is just one vertex v for which n_v ≤ 1/2(n-1) (the centroid or centroid tree) or there are two adjacent vertices v and w for which n_v = n_w = 1/2n(the bicentroid or bicentroid tree). It is easy to see that every tree is either centroidal or bicentroidal, but not both.
Note that we can think of the centroid or bicentroid as the 'center of gravity' of the tree.
For example, given a following tree

Since n_c = 4, n_e = 4, n_f = 5 and n_g = 6. Therefore, we have a bicentroidal tree with bicentroid ce.


Another example, given a following tree.

Since n_b = 6, n_c = 5, n_d = 3 and n_f = 5. Therefore,  we have a centroidal tree with centroid d.


Tree Searching
There are two well-known search methods. They are brown as depth-first search( DFS) and breadth-first search (BFS). Each of these methods lists the vertices as they are encountered, and indicates the direction in which each edge is first traversed. The methods differ only in the way in which the vertex-lists are constructed.

Depth-First Search (DFS)
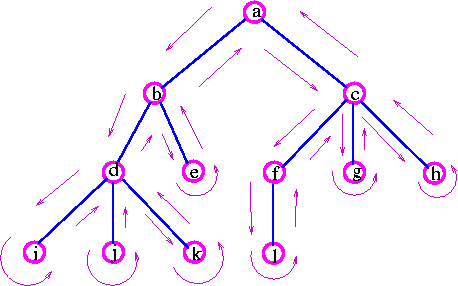
The basic idea of depth-first search is to penetrate as deeply as possible into a tree before fanning out to other vertices. This idea may be depicted as follows:

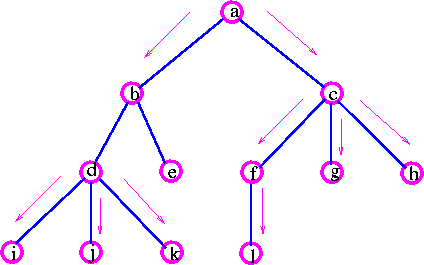
a -> b --> d --> i -> j -> k -> e -> c -> f -> i -> g  -> h.

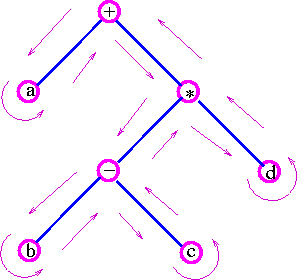
Another example, the expression a + {(b-c) × d} can represented by following tree:

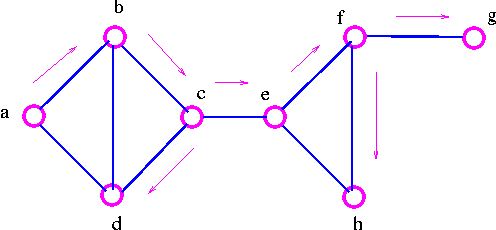
Example: Consider the graph

Note that we have marked those edges we used when going to new vertex. These edges form a spanning tree, called a DFS spanning tree.


Breadth-First Search (BFS)
The basic idea of breadth-first search is to fan out to as many vertices as possible before penetrating deep into a tree. This idea may be depicted as follows:

a --> b --> c --> d --> e --> f --> g --> h --> i --> j --> k --> e
above example clearly shows that breadth-first search must complete each level before proceeding to the next one.
Example: Consider the graph

Note that we have marked those edges we used when going to new vertex. These edges form a spanning tree, called a BFS spanning tree.

Euler Graphs......

Euler Graphs

Consider the following road map

The explorer's Problem: An explorer wants to explore all the routes between a number of cities. Can a tour be found which traverses each route only once? Particularly, find a tour which starts at A, goes along each road exactly once, and ends back at A.
Examples of such tour are

A

B

C

D

E

F

B

G

C

E

G

F

A

A

F

G

C

D

E

G

B

C

E

F

B

A

The Explorer travels along each road (edges) just once but may visit a particular city (vertex) several times.

The Traveler's Problem
A traveler wants to visit a number of cities. Can a tour be found which visits each city only once? Particularly, find a tour which starts at A, goes to each city exactly once, and ends back at A.
Examples of such tour are

A	B	C	D	E	G	F	A
A	F	E	D	C	G	B	A

The travelers visits each city (vertex)  just once but may omit several of the roads (edges) on the way.

Eulerian Trail
A connected graph G is Eulerian if there is a closed trail which includes every edge of G,  such a trail is called an Eulerian trail.

Hamiltonian Cycle
A connected graph G is Hamiltonian if there is a cycle which includes every vertex of G; such a cycle is called a Hamiltonian cycle.
Consider the following examples:

This graph is BOTH Eulerian and Hamiltonian.

This graph is Eulerian, but NOT Hamiltonian.

                                                                                                        

 
This graph is an Hamiltionian, but NOT Eulerian.

This graph is NEITHER Eulerian NOR Hamiltionian

Theorem     Let G be a connected graph. Then G is Eulerian if and only if every vertex of G has even degree.

• Necessary Condition
  • If G is Eulerian, then every vertex of G has even degree.
• Sufficient Condition
  • If every vertex of G has even degree, then G is Eulerian.

Eulerian-Type Problems

• Edge-traceable graphs.
• Diagrams-Tracing Puzzles.
• Dominoes.
• Mazes and labyrinths,
• The Chinese Postman Problem.
• The Rotating Drum Problem.

Neither necessary nor sufficient condition is known for a graph to be Hamiltonian. The search for necessary or sufficient conditions is a major area of study in graph theory today.

Sufficient Condition

Dirac's Theorem    Let G be a simple graph with n vertices where n ≥ 3 If deg(v) ≥ 1/2 n for each vertex v, then G is Hamiltonian.
For example,

n = 6 and deg(v) = 3 for each vertex, so this graph is Hamiltonian by Dirac's theorem.

Ore's Theorem    Let G be a simple graph with n vertices where n ≥ 2 if deg(v) + deg(w) ≥ n for each pair of non-adjacent vertices v and w, then G is Hamiltonian.
For example,

n = 5 but deg(u) = 2, so Dirac's theorem does not apply. However, deg(v) + deg(w) ≥ 5 for all pairs of vertices v and w (infact, for all pairs of vertices v and w), so this graph is Hamiltonian by Ore's theorem.
Note that if deg(v) ≥ 1/2 n for each vertex, then deg(v) + deg(w) ≥ n for each pair of vertices v and w. It follows that Dirac's theorem can be deduced from Ore's theorem, so we prove only Ore's threoem.


Hamiltonain - Type Problem

• Gray Codes.
• The Traveling Salesperson Problem
• Ranking in Tournaments.

Graph Theory Definitions

Definitions and Examples

Informally, a graph is a diagram consisting of points, called vertices, joined together by lines, called edges; each edge joins exactly two vertices. A graph G is a triple consisting of a vertex set of V(G), an edge set E(G), and a relation that associates with each edge two vertices (not necessarily distinct) called its endpoints.

Definition of Graph
 A graph G = (V, E) consists of a (finite) set denoted by V, or by V(G) if one wishes to make clear which graph is under consideration, and a collection E, or E(G), of unordered pairs {u, v} of distinct elements from V. Each element of V is called a vertex or a point or a node, and each element of E is called an edge or a line or a link.
Formally, a graph G is an ordered pair of dsjoint sets (V, E), where E Í V × V. Set V is called the vertex or node set, while set E is the edge set of graph G. Typically, it is assumed that self-loops (i.e. edges of the form (u, u), for some u Î V) are not contained in a graph.

Directed and Undirected Graph
A graph G = (V, E) is directed if the edge set is composed of ordered vertex (node) pairs. A graph is undirected if the edge set is composed of unordered vertex pair.

Vertex Cardinality
The number of vertices, the cardinality of V, is called the order of graph and devoted by |V|. We usually use n to denote the order of G. The number of edges, the cardinality of E, is called the size of graph and denoted by |E|. We usually use m to denote the size of G.

Neighbor Vertex and Neighborhood
We write v_iv_j Î E(G) to mean {v_i, v_j}ΠE(G), and if e = v_i v_j Î E(G), we say v_i and v_j are adjacent.
Formally, given a graph G = (V, E), two vertices  v_i , v_j Î V are said to be neighbors, or adjacent nodes, if ( v_i , v_j ) Î E. If G is directed, we distinguish between incoming neighbors of v_i (those vertices v_j Î V such that (v_j, v_i) Î E) and outgoing neighbors of v_i (those vertices v_j ÎV such that (v_i, v_j) Î E).

The open neighborhood N(v) of the vertex v consists of the set vertices adjacent to v, that is, N(v) = {w Î v : vw Î E}. The closed neighborhood of v is N[v] = N(v) È {v}. For a set S Í V, the open neighborhood N(S) is defined to be U_vÎSN(v), and the closed neighborhood of S is N[S] = N(S) È S.

Vertex Degree
The degree deg(v) of vertex v is the number of edges incident on v or equivalently, deg(v) = |N(v)|. The degree sequence of graph is (deg(v₁), deg(v₂), ..., deg(v_n)), typically written in nondecreasing or nonincreasing order. The minimum and maximum degree of vertices in V(G) are denoted by d(G) and ∆(G), respectively. If d(G) = ∆(G) = r, then graph G is said to be regular of degree r, or simply r-regular.
Formally, given a graph G = (V, E), the degree of a vertex v Î V is the number of its neighbors in the graph. That is,
                                            deg(v) = | {u Î V : (v, w) Î E}|.
If G is directed, we distinguish between in-degree (nimber of incoming neighbors) and out-degree (number of outgoing neighbors) of a vertex.

Loop and Multiple Edges
A loop is an edge whose endpoints are equal i.e., an edge joining a vertex to it self is called a loop. We say that the graph has multiple edges if in the graph two or more edges joining the same pair of vertices.

Simple Graph
A graph with no loops or multiple edges is called a simple graph. We specify a simple graph by its set of vertices and set of edges, treating the edge set as a set of unordered pairs of vertices and write e = uv (or e = vu) for an edge e with endpoints u and v.

When u and v are endpoints of an edge, they are adjacent and are neighbors.


Connected Graph
A graph that is in one piece is said to be connected, whereas one which splits into several pieces is disconnected.

A graph G is connected if there is a path in G between any given pair of vertices, otherwise it is disconnected. Every disconnected graph can be split up into a number of connected subgraphs, called components.

Subgraph
Let G be a graph with vertex set V(G) and edge-list E(G). A subgraph of G is a graph all of whose vertices belong to V(G) and all of whose edges belong to E(G). For example, if G is the connected graph below:

where V(G) = {u, v, w, z} and E(G) = (uv, uw, vv, vw, wz, wz} then the following four graphs are subgraphs of G.

Degree (or Valency)
Let G be a graph with loops, and let v be a vertex of G. The degree of v is the number of edges meeting at v, and is denoted by deg(v).
For example, consider, the following graph G

The graph G has deg(u) = 2, deg(v) = 3, deg(w) = 4 and deg(z) = 1.


Regular Graph
A graph is regular if all the vertices of G have the same degree. In particular, if the degree of each vertex is r, the G is regular of degree r.

The Handshaking Lemma    In any graph, the sum of all the vertex-degree is equal to twice the number of edges.

Proof    Since each edge has two ends, it must contribute exactly 2 to the sum of the degrees. The result follows immediately.
The Following are the consequences of the Handshaking lemma.

1. In any graph, the sum of all the vertex-degree is an even number.
2. In any graph, the number of vertices of odd degree is even.
3. If G is a graph which has n vertices and is regular of degree r, then G has exactly 1/2 nr edges.

Isomorphic Graphs
Two graph G and H are isomorphic if H can be obtained from G by relabeling the vertices - that is, if there is a one-to-one correspondence between the vertices of G and those of H, such that the number of edges joining any pair of vertices in G is equal to the number of edges joining the corresponding pair of vertices in H. For example, two unlabeled graphs, such as

are isomorphic if labels can be attached to their vertices so that they become the same graph.

The word isomorphic derives from the Greek for same and form.


Walk
A walk of length k in a graph G is a succession of k edges of G of the form uv, vw, wx, . . . , yz.

We denote this walk by uvwx . . yz and refer to it as a walk between u and z.


Trail and Path
If all the edges (but no necessarily all the vertices) of a walk are different, then the walk is called a trail. If, in addition, all the vertices are difficult, then the trail is called path.

• The walk vzzywxy is a trail since the vertices y and z both occur twice.
• The walk vwxyz is a path since the walk has no repeated vertices.

Complete Graphs
A computer graph is a graph in which every two distinct vertices are joined by exactly one edge. The complete graph with n vertices is denoted by  K_n.
The following are the examples of complete graphs.

    

The graph K_n is regular of degree n-1, and therefore has 1/2n(n-1) edges, by consequence 3 of the handshaking lemma.

Null Graphs
A null graphs is a graph containing no edges. The null graph with n vertices is denoted by N_n.
The following are the examples of null graphs.

Note that N_n is regular of degree 0.


Cycle Graphs
A cycle graph is a graph consisting of a single cycle. The cycle graph with n vertices is denoted by C_n.
The following are the examples of cyclic graphs.

Note that  C_n is regular of degree 2, and has n edges.

Path Graphs
A path graph is a graph consisting of a single path. The path graph with n vertices is denoted by P_n.
The following are the examples of path graphs.

Note that path graph, P_n, has n-1 edges, and can be obtained from cycle graph, C_n, by removing any edge.


Bipartite Graphs
A bipartite graph is a graph whose vertex-set can be split into two sets in such a way that each edge of the graph joins a vertex in first set to a vertex in second set.
The examples of bipartite graphs are:

Complete Bipartite Graph
A complete bipartite graph is a bipartite graph in which each vertex in the first set is joined to each vertex in the second set  by exactly one edge. The complete bipartite graph with rvertices and 3 vertices is denoted by K_r,s.
The following are some examples.

Note that K_r,s has r+s vertices (r vertices of degrees, and s vertices of degree r), and rs edges. Note also that  K_r,s = K_s,r.
An Important Note:    A complete bipartite graph of the form K_r,s is called a star graph.

Cube Graph
The cube graphs is a bipartite graphs and have appropriate in the coding theory.
The cube graphs constructed by taking as vertices all binary words of a given length and joining two of these vertices if the corresponding binary words differ in just one place. The binary words of length k is called the k-cube (or k-dimensional cube) graph and is denoted by Q_k.
The following are some examples.

Note that Q_k has 2^k vertices and is regular of degree k. It follows from consequence 3 of the handshaking lemma that Q_k has k* 2^k-1 edges.


The Peterson Graph
This graph is named after a Danish mathematician, Julius Peterson(1839-1910), who discovered the graph in a paper of 1898.

Tree Graph
A tree is a connected graph which has no cycles.

Spanning Tree
If G is a connected graph, the spanning tree in G is a subgraph of G which includes every vertex of G and  is also a tree.
Consider the following graph

The following are the three of its spanning trees:

Interval Graphs
Consider the intervals (0, 3), (2, 7), (-1, 1), (2, 3), (1, 4), (6, 8) which may be illustrated as

We can construct the resulting interval graphs by taking the interval as vertices, join two of these vertices by an edge whenever the corresponding intervals have at least one point in common.

Note that since the intervals (-1, 1) and (1, 4) are open intervals, they do not have a point in common.


Definition of Diagraph
A directed graph or diagraph D consists of a set of elements, called vertices, and a list of ordered pairs of these elements, called arcs. The set of vertices is called arcs. The set of vertices is called the vertex-set of D, denoted by V(D), and the list of arcs is called the arc-list of D, denoted by A(D). If v and w are vertices of D, then an arc of the form vw is said to be directed from v to w, or to join v to w.

 The underlying graph of diagraph is the graph obtained by replacing each arc of diagraph by corresponding (undirected) edge. For example, consider the following digraph

The underlying graph of the above digraph is

The Platonic Graphs
The following regular solids are called the Platonic solids:

Tetrahedron

Hexahedron (cube)

Octahedron

Dodecahedron

Icosahedron

The name Platonic arises from the fact that these five solids were mentioned in Plato's Timaeus. A Platonic graph is obtained by projecting the corresponding solid on to a plane.